运放有哪些噪声源?什么是噪声频率曲线?什么是等效输入噪声?噪声和带宽是什么关系?什么是闪烁噪声、什么是白噪声?
本文章带你一次看个够,千字长篇分析,仿真文件已经整理得明明白白,先收藏,后阅读。
我们先从电阻热噪声说起,图1-1 是使用multisim做的理想电阻仿真结果,理想电阻只有电阻值这个参数,没有考虑电阻的噪声,两个10kΩ的电阻对1V直流电压分压,结果就是500mV。
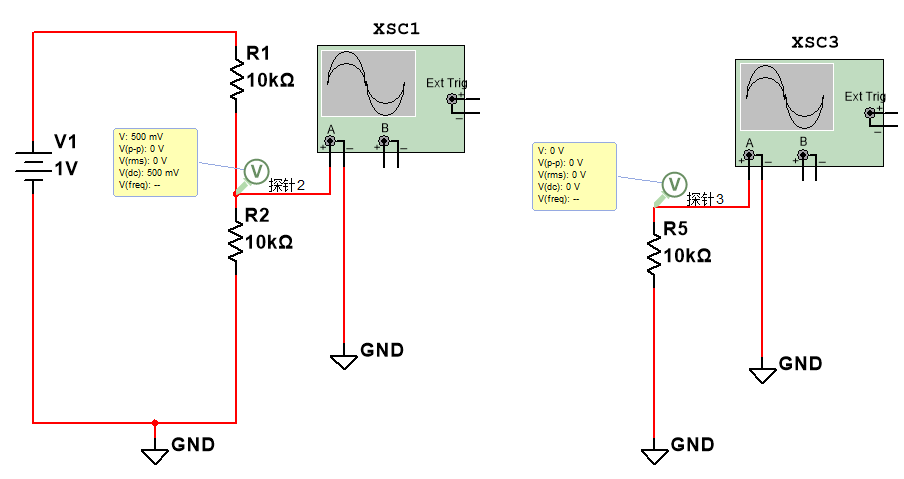
图1-1 理想电阻仿真
图1-2 是仿真结果,当电路开路时,电阻两端也是没有电压的,是0V。无论是万用表还是示波器的交流档,交流测试结果都是0V。
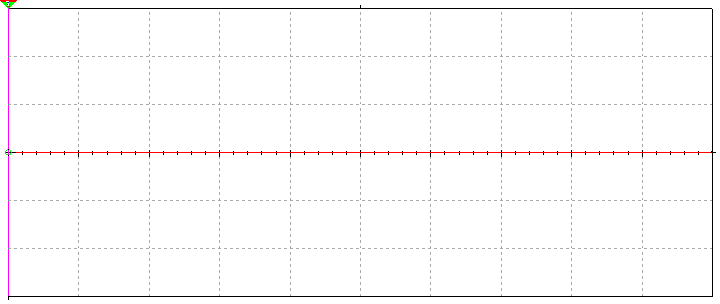
图1-2 理想电阻仿真结果
下面我们加入电阻的热噪声看下结果,电阻热噪声在库中的位置参考图1-3 。
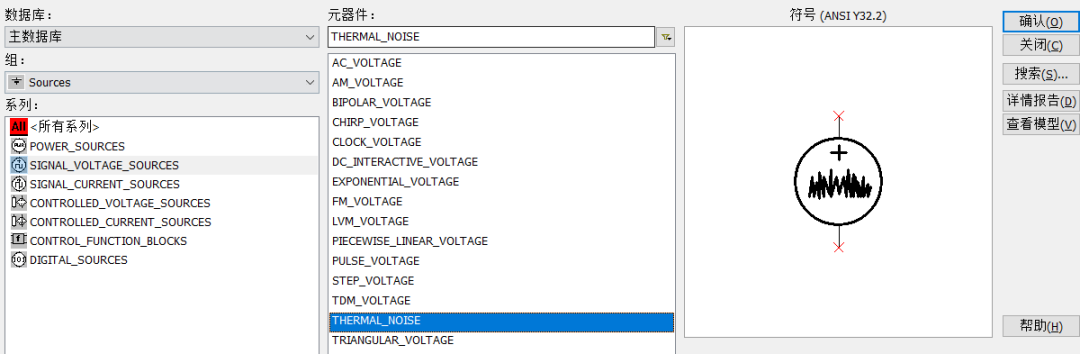
图1-3加入电阻热噪声
图1-4 是加入电阻热噪声的仿真原理图,电阻是10KΩ,频带范围是100KHz,此时电阻即使是开路状态,也会在两端产生电压波动,产生噪声,用万用表交流档测量电阻两端电压有效值是4uV,电阻两端开路时热噪声计算公式如下:
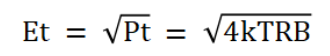
k是玻尔兹曼常数,k=1.38*10-23 J/K,T是开尔文热力学温度,R是电阻值,B是系统等效噪声带宽。
举例:
当温度是27℃(300开尔文)时,10KΩ的电阻,在带宽为100KHz放大电路中,电阻两端的开路热噪声电压有效值是4uV。这个结果我们仿真的结果一致,上面的公式也说明了电阻越大噪声越大,这也就是我们基于运算放大器来设计电路时,电阻不要太大,基本以KΩ为单位,如果电阻大那么电阻引入的噪声也就会大。
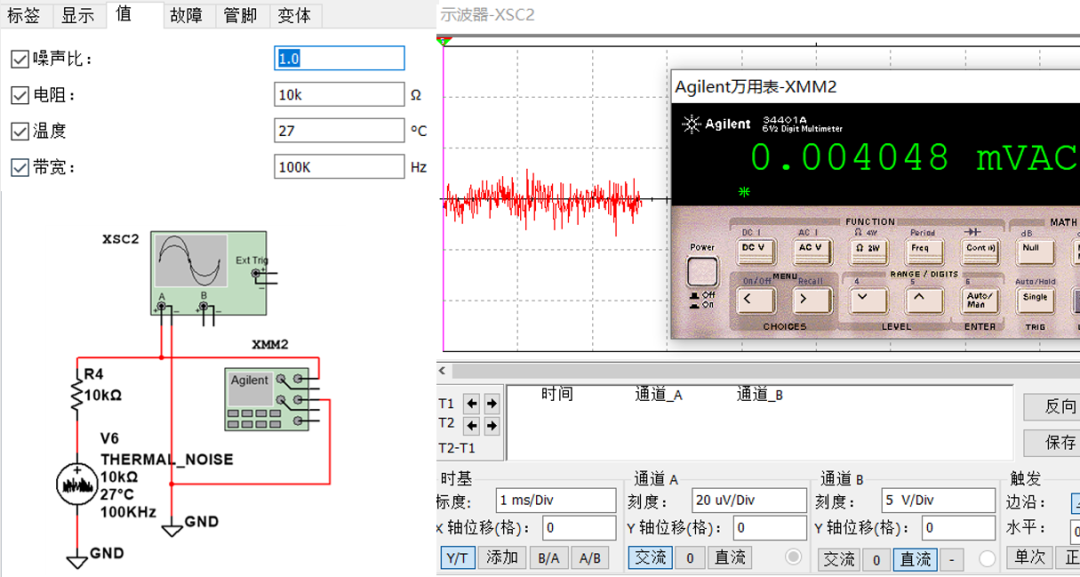
图1-4 电阻热噪声仿真结果
说完电阻我们在来说运算放大器,图1-5 是AD8599的噪声参数,主要有三种噪声:0.1Hz-100Hz的峰峰值噪声、超过1KHz的电压噪声密度、电流噪声密度。我们这里以低频峰峰值噪声和电压噪声为主要介绍对象。

图1-5 运放噪声参数
图1-6 是运放的噪声曲线,几乎每一个运放都会给出这样的曲线图,第一行是时域的峰峰值噪声图,主要以0.1Hz-10Hz为主(加入了滤波功能,只观察0.1Hz-10Hz这部分的噪声),这一部分以闪烁噪声为主,闪烁噪声随着频率的增加越来越小,与频率成反比,见图中的第二行图起始位置,因此也被叫做1/f噪声。而随着频率的增加,1/f噪声减小,而白噪声的作用就变成主要噪声了。
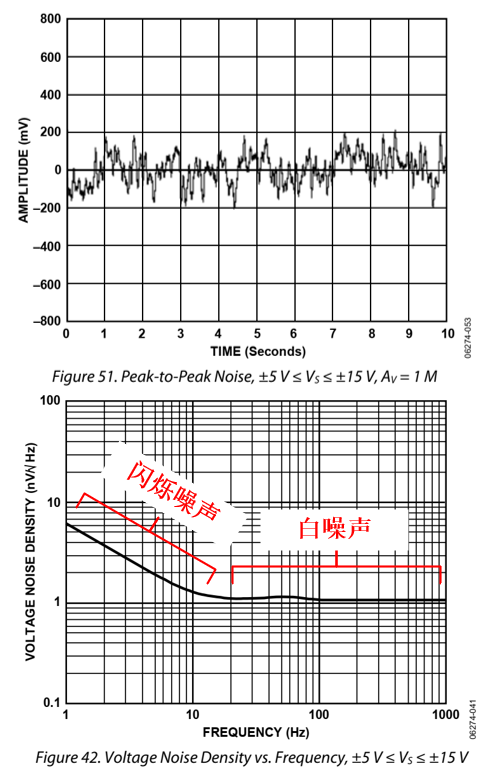
图1-6 运放噪声曲线
图1-6 中的噪声曲线实际是1/f与白噪声的合成,见图1-7 ,我们通过曲线可以计算1/f噪声与白噪声的大小,来评估电路的噪声情况。
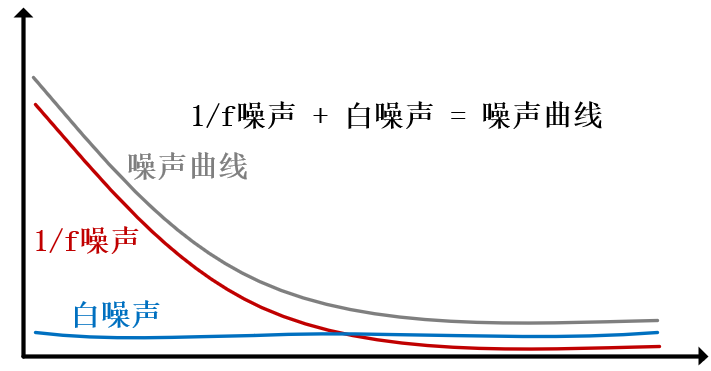
图1-7运放噪声曲线的合成
话不多说,说多了太抽象,枯燥无味,我们直接用multisim来画出手册中的噪声曲线。仿真参数和电路见图1-8 ,一个简单的跟随器,运放的输出等于输入,仿真频率与手册中的曲线保持一致,选择为1Hz-1000Hz。
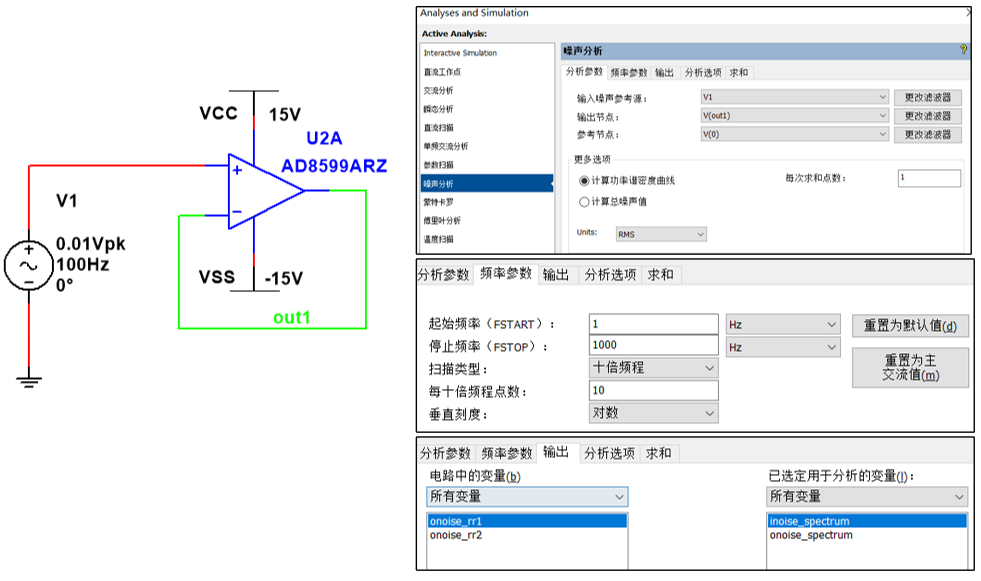
图1-8运放噪声仿真
我们对比手册中的曲线和我们仿真的曲线,见图1-9 这两条曲线虽然称不上“一毛一样”,但是说它们“两毛一样”大家应该认同吧,比如在1Hz时噪声密度是大约是5.9nV/√Hz,在1KHz时噪声密度大约是1nV/√Hz,仿真结果与手册是非常接近的。其中仿真结果其实是有两条曲线的,一条是输入噪声曲线,一条是输出噪声曲线,由于仿真的是电压跟随器,噪声增益(同相比例放大倍数)为1,因此输入输出就一样了。
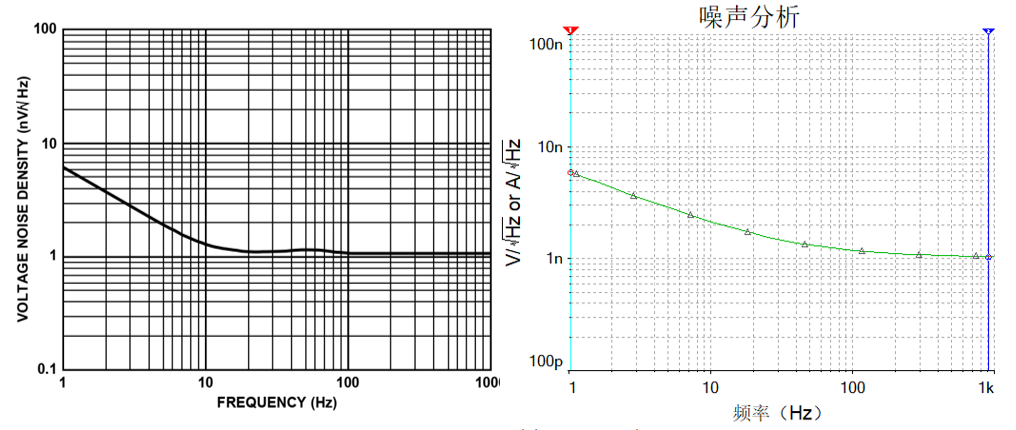
图1-9 运放噪声仿真结果1
我们把电路放大倍数设置为10倍,仿真结果见图1-10 ,此时输入噪声和输出噪声就刚好相差10倍。
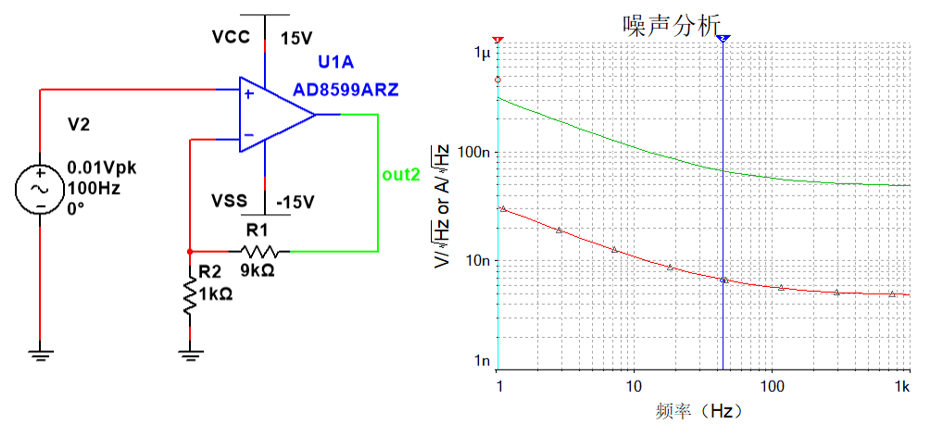
图1-10运放噪声仿真结果2
我们继续以10倍放大电路为研究对象,这次咱们仿真下噪声有效值,并且看下怎么通过电压曲线图来手动计算这个有效值,仿真电路和参数设置见图1-11 。
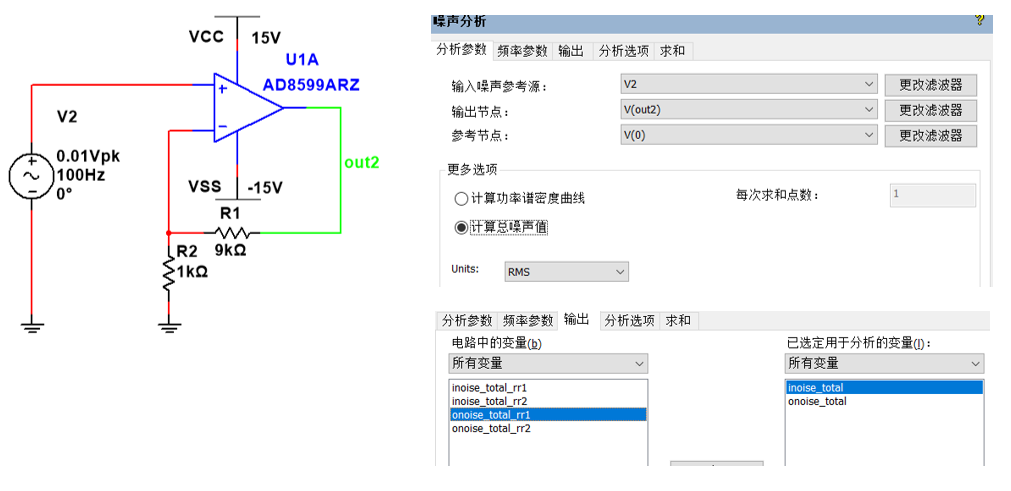
图1-11运放噪声仿真结果3
仿真的结果我放到了图1-12 ,可以看到不管是噪声曲线还是噪声有效值仿真,输出与出入都相差了10倍。计算噪声有效值,我们需要分别结算白噪声有效值Uw和1/f噪声的有效值Uf,然后再求二者的总噪声贡献。
我这里直接抛出公式:
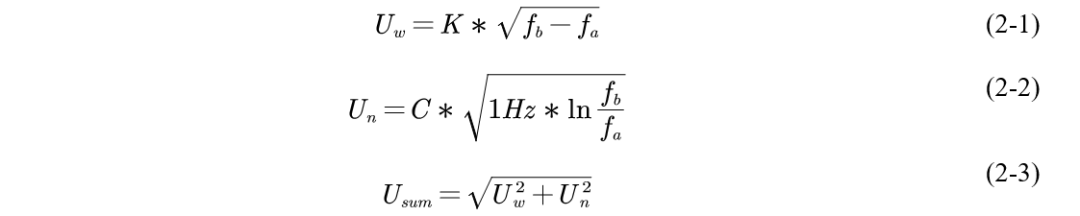
只需要3个公式就可以了,其中Uw是白噪声有效值,Un是1/f噪声有效值,fb是上限频率,仿真里和手册里都是1000Hz,fa是下限频率,仿真里和手册里都是1Hz。我们需要单独看下K和C是怎么来的。在图1-12 中,我们看红色曲线(输入噪声曲线),取曲线的最终平稳位置的噪声密度值就是K,图中大约是4.9 nV/√Hz,根据公式2-1,就可以计算出Uw大约是4.9*√(1000-1)=154.87nV。
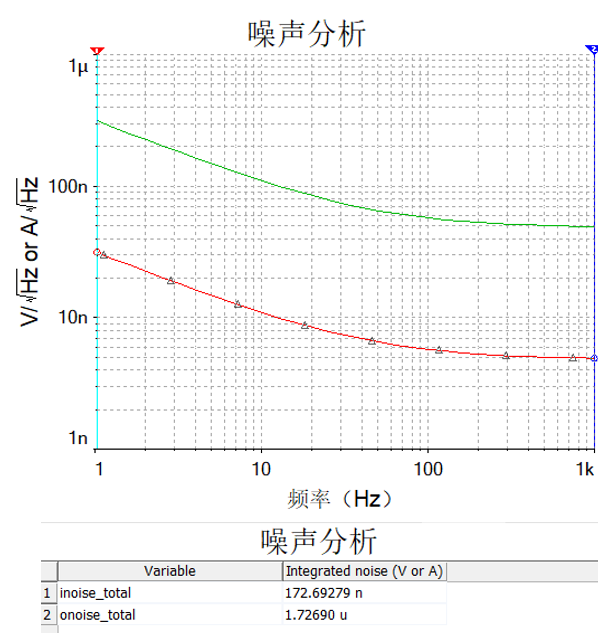
图1-12运放噪声仿真结果4
C是多少呢?在图1-12 红色输入噪声曲线中,取频率为1Hz时的噪声密度值就是C,图中大约是31.32 nV/√Hz,根据公式2-2就可以计算出Un大约是31.32* √ln(1000)=82.32nV。
那么,我们就得到Uw=154.87nV,Un=82.32nV,(可见白噪声贡献大于1/f噪声),根据公式2-3就可以得到总噪声了,Usum=√(284.462+82.322)=175.38nV。
我们计算的输入噪声有效值是175.38nV,而仿真的结果是172.69nV,仿真与计算基本是一致的。
同样的道理,我们也可以通过手册的噪声频率曲线来计算放大倍数为1时的噪声有效值,原理都是一样的。
*博客内容为网友个人发布,仅代表博主个人观点,如有侵权请联系工作人员删除。